Liczby palindromiczne
Gdy cyfry w lustrze mówią dokładnie to samo.
Przeciętny program nauczania matematyki jest raczej ograniczony pod względem rodzajów liczb, które są prezentowane uczniom. Z pewnością uczniowie wiedzą o liczbach nieparzystych, parzystych, liczbach pierwszych, a nawet o liczbach doskonałych, które omówimy w dalszej części tego rozdziału. Istnieją jednak inne rodzaje liczb, które mają niezwykłe własności i są często pomijane – mianowicie liczby, które czytamy tak samo w obie strony.
Są one nazywane liczbami palindromicznymi, czytamy je tak samo z lewej strony do prawej, jak i z prawej do lewej. Palindromem może być też słowo, fraza lub całe zdanie.
Palindromem w matematyce są na przykład liczby 666 lub 12321, które czyta się tak samo w każdym kierunku.
Pierwsze potęgi liczby 11 dają piękną piramidę palindromów:
111 = 11
112 = 121
113 = 1331
114 = 14641
Interesujące jest to, jak można wygenerować palindrom z losowo wybranej liczby. Wystarczy ciągle dodawać liczbę do jej odwrócenia (czyli liczby z tymi samymi cyframi, ale zapisanymi w odwrotnej kolejności), aż dotrzemy do palindromu.
Przykłady:
23 + 32 = 55 (palindrom)
2 kroki
75 + 57 = 132
132 + 231 = 363 (palindrom)
3 kroki
86 + 68 = 154
154 + 451 = 605
605 + 506 = 1111 (palindrom)
6 kroków
start: 97 → palindrom po 6 dodaniach
24 kroki
start: 98 → palindrom dopiero po 24 dodaniach
Dla dwucyfrowej liczby ab, gdzie a ≠ b, suma cyfr a + b często zdradza liczbę potrzebnych kroków.
Szczególną rolę odgrywa liczba 196. Gdy rozpoczynamy od niej proces „odwróć i dodaj”, do tej pory nie udało się uzyskać palindromu, mimo że wykonano już ponad trzy miliony dodawań z odwróconą liczbą. Wciąż nie wiadomo, czy z tej liczby kiedykolwiek otrzymamy palindrom.
Jeśli zastosujemy procedurę do liczby 196, to w szesnastym kroku pojawia się liczba 227 574 622, którą uzyskamy także w piętnastym kroku w drodze do palindromu, gdy zaczniemy od liczby 788. Oznaczałoby to, że zastosowanie procedury do liczby 788 również nigdy nie da palindromu.
Wśród pierwszych stu tysięcy liczb naturalnych znajduje się aż 5996 takich, dla których nie udało się jeszcze wykazać, że proces „odwróć i dodaj” prowadzi do palindromu. Przykłady: 196, 691, 788, 887, 1675, 5761, 6347, 7436.
Dzięki opisanej procedurze widać, że niektóre liczby dają ten sam palindrom w tej samej liczbie kroków. Na przykład z liczb 554, 752, 653 otrzymujemy ten sam palindrom 11011 w trzech krokach.
Ogólnie rzecz biorąc, wszystkie liczby całkowite, w których odpowiednie pary cyfr symetrycznych względem środkowej cyfry 5 mają taką samą sumę, wytworzą ten sam palindrom w tej sameej liczbie kroków.
Zdarza się też, że różne liczby dochodzą do tego samego palindromu, ale w innej liczbie kroków. Na przykład zaczynając od liczby 198, otrzymamy palindrom 79497 w pięciu krokach, natomiast z liczby 7299 – już w dwóch.
– dla liczby ab (a ≠ b) suma cyfr a + b często zdradza liczbę kroków.
Przykłady minimalnej liczby kroków do palindromu dla liczb dwucyfrowych:
11, 12, 13, 14, 15, 16, 17 → odpowiednio: 1, 2, 2, 3, 4, 6, 24 kroków.
Gdyby temat liczb palindromicznych pojawił się w szkole, można by szybko zachwycić się kilkoma pięknymi wzorami. Niektóre liczby palindromiczne po podniesieniu do kwadratu wciąż pozostają palindromami:
2122 = 44 944
To jednak wyjątki – np. 5452 = 297 025, co palindromem już nie jest.
Są też liczby niepalindromiczne, których kwadraty tworzą palindrom:
8362 = 698 896
Innym rodzajem palindromów są liczby złożone wyłącznie z jedynek – tzw. repunits. Wszystkie takie liczby zawierające mniej niż dziesięć jedynek po podniesieniu do kwadratu dają palindrom, np.:
Istnieją też palindromiczne liczby, których sześciany również są palindromami. Liczby te można zapisać w postaci n = 10k + 1, gdzie k = 1, 2, 3...:
k = 2, n = 101 → 1013 = 1 030 301
k = 3, n = 1001 → 10013 = 1 003 003 001
Gdy liczba n składa się z trzech jedynek i dowolnej parzystej liczby zer umieszczonych symetrycznie między nimi, to n3 jest palindromem:
10 1013 = 1 030 607 060 301
1 001 0013 = 1 003 006 007 006 003 001
1 0001 00013 = 1 000 300 006 000 700 006 000 300 001
Jeśli n składa się z czterech jedynek i zer w układzie palindromicznym, ale odległości między jedynkami nie są jednakowe, to n3 także jest palindromem:
10 100 1013 = 10 303 319 093 390 913 303 01
Gdy natomiast pomiędzy jedynkami pojawia się wszędzie taka sama liczba zer, sześcian liczby zwykle nie jest palindromem, np. 1 010 1013 = 1 030 610 121 210 060 301.
Ciekawostka: liczba 2201 jest jedyną niepalindromiczną liczbą mniejszą od 280 000 000 000 000, której sześcian jest palindromem:
Dla zabawy popatrzmy na następujący wzór z liczbami palindromicznymi:
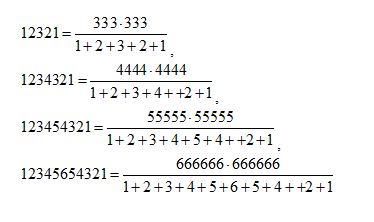
…i tak dalej. Z takich cegiełek można budować całe „pałace” z palindromów.

